温特线性和季节性指数平滑法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第454页（976字）

一种较高级形式的平滑法。

由温特始于60年代初创立。这种方法与二次指数平滑法所不同的是，具有使季节性修正和趋势性修正相结合的特殊优点。因此，它能用于对既有趋势模式又有季节性模式的数据序列进行预测。

温特线性和季节性指数平滑法，以三个方程式为基础，每一个方程式所平滑的参数，都与模式的三个组成部分(随机、线性、季节性)之一有关系。在这方面，它和二次指数平滑法相似，可平滑随机性和修正趋势性。但是，温特法还包括一个处理季节性的附加参数。

温特法的三个基本方程式是：

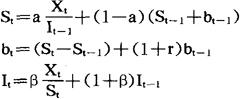
式中L是季节性长度(如一千的目数或季度数)；I是季节性修正数。I_t的方程式相当于季节性指数。

该指数是数列的现值X_t与数列的一次平滑现值S_t之比。

假如X_t大于S_t，则比值大于1，假如X_t小于S_t则比值小于1。认识到S_t是数列的一次平滑(平均值)，而且不包括季节性这一点，对于了解这种方法和季节性指数I_t的作用是极为重要的。另一方面，数据值X_t中却包括季节性。

而且，还包括了数列中的某些随机性。为了要使这种随机性得到平滑，I_t方程式以β对重新计算的季节性系数(X_t／S_t)加权，以(1－β)对同一季节I_t－1的最新季节数加权。

b_t的方程式只是使趋势平滑，因为它的r对增量趋势(S_t－S_t－1)加权，以(1－r)对以前的趋势值(b_t－1)加权。在平滑后的S_t的方程式中，第一项要除的季节数I_t－1，其目的是消除X_t的季节波动。

将X_t用大于1的数去除，得出的数值比原始数值小一个百分数，这一百分数恰好等于第t－1时间间隔且高于均值的季节值。当季节性数值小于1时，将会出现相反的修正情况。

因为在未求出S_t之前无法计算It值，因而在计算中均用I_t－1值。

伴随着使用温特方法的一个问题是，要确定能使均方误差(WSE)最小化的α、β和γ各值。

唯一能做到这点的方法是逐次逼近法。寻求最佳值的做法是，首先是对各参数确定可能减少均方误差的数值变化方向。参数值可按逐步增加的方式使其变化，以求出可以得到最小均方误差的各值。