系统模型方法

出处：按学科分类—工业技术 企业管理出版社《工程师手册》第256页（2545字）

1．系统模型及其特征

系统设计的对象非常广泛，而且有些还非常复杂和庞大。因此，对系统进行分析、研究，作出有说服力的结果，往往需要利用模型来反映实体。

实体是一切客观事物及其运动形态的总称。而模型则是对实体的特征和变化规律的定量的抽象表述，是对所要研究的特定特征的定量抽象的表述，能在所要研究的主题范围内更普遍、更集中、更深刻地描述实体的特征。但是，模型不是实体本身，不能等同于实体，它是实体的抽象，反映着实体的主要特征而又高于实体，具有同类问题的共性。因此，归结起来，系统模型具有三个特征：(1)是系统的抽象或模仿；(2)是由说明系统本质和特征的诸因素所构成；(3)它集中表明各因素间的关系。一般系统模型的表达式为

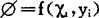
式中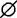，描述系统目标、功能或效果，称为目标函数(一般总希望其达到最大或最小值)；x_i为可控变量(x_i可以有约束方程或不等式表示其有一定的取值范围)，常称为约束条件；y_i是一些不可控因素或状态，对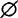有影响。

2．系统模型的种类

按抽象化程度，系统模型可分为结构模型、数学模型和模拟模型。其中，结构模型是以物理特征、图解和逻辑的形式反映系统的结构或功能关系。例如，建筑物的沙盘造型；方框图；信号流图；电路图；程序操作顺序图表等。

数学模型是把系统中诸因素间的关系用数字的形式描述出来。它能深刻地反映出客观事物的数量关系和本质规律。由于数学模型可使客观事物抽象化、形象化，因而有助于抓住事物的本质，以及有助于把握事物的整体。为此，在系统分析中多数用数学模型来定量说明系统的目的。能用代数式、微分、差分方程、函数方程、传递函数描述的系统，称为确定性模型；能用概率分布、相关函数、频谱密度、存取矩阵、马尔克夫链等描述的系统，称为概率性模型。

模拟模型是利用一组可控制的条件来代替实体，通过模仿性的试验来了解实体的本质和规律。应用最多的有：(1)利用模拟计算机或专用摸拟机进行的模拟式模拟，如研究用的核反应堆、生产过程、网络等；(2)利用数字计算机进行的数字式模拟，如用蒙特卡洛法处理随机过程、功能系统等；(3)模拟一数字混合模拟，它是同时用连续量和离散量所进行的模拟过程，如对含有过程参量系统的描述等。

3．构造系统模型的原则

由于研究系统的范围和性质的不同，构造系统的模型方法也千差万别。实际上，要想构造一个系统模型，必须对研究的系统进行大量的周密的调查，去粗取精，去伪存真，找出主要影响因素，剔除次要影响因素，进而利用系统所属学科的知识，建立起影响系统目标的因素间的相互关系，有些则依据系统反映出的规律，经过统计而形成模型。企图采用条条框框的规定，就会限制创造模型的可能。为此，与其说构造系统模型是一种技术，莫如说是一种艺术，其关键在于掌握一些基本原则，灵活运用。这些原则是：(1)将所研究的事或物规划成系统；(2)分析影响系统性质的诸因素；(3)确定主要影响因素；(4)确定因素间的逻辑关系，进而用数字的手段来描述这种关系；(5)通过分解，子系统化；(6)子系统模型化；(7)综合部分子系统模型；(8)全系统模型化。

4．构造系统模型数值例

例如，某厂生产某种单一产品，假定成本已知，且预测到需求量。试问，其盈亏将受到什么影响?如果需求量变化，盈亏将受到什么影响?可变成本上升，利润又将受到什么影响?为说明这些问题，依构造系统模型的原则，可以构造它的数学模型。其步骤是：第一步，规划系统。这是自产自销的系统，其分析如框图2．1．6－1。第二步，分析影响系统目标的因素，且找出主要影响因素，即成本、销售收入和盈利。第三步，确定因素间的逻辑关系，如图2．1．6－2。第四步，用参量来描述逻辑关系，即

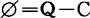
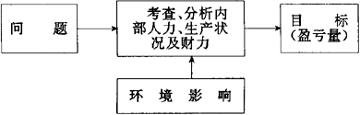
图2．1．6－1 产销系统

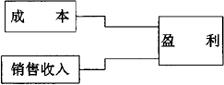
图2．1．6－2 系统逻辑图

显然，若想利润大，有两条途径，一是通过广开门路(系统环境)，采用薄利多收等增加销售收入Q；二是减少消耗，压缩辅助开支降低成本C。第五步，则是深入分析，分解成子系统。这里是分解参量，即

Q=Px

C=f+C₁x

上式中，P为产品单价，x为销售量，f为固定成本，C₁为单件产品的可变成本。

构成模型的最后一步，是综合部分系统模型化。首先，确定目标函数解析式，即求

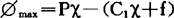
=(p－C₁)x－f

=Kx－f

式中K=P－C₁，称为净值。然后，确定约束条件。从内部看，销售量x靠生产来控制，即受到生产能力的约束。如只能生产m件，则x≤m。从外部环境看，它受市场的制约。若预测到需求量为n，则x≤n，且有x不能为负，即不应造废次品，则x＞0。作为数值例，假定P=3．5(元)，C₁=2(元)，m=300(件)，n=200(件)，则净值K=3．5－2=1．5，数学模型为求：

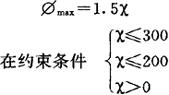
依此可描述成图2．1．6－3。当然，这只是为了说明构造系统模型的思考方法，所以分析得很简练。而实际上，对成本、销售收入还应进行详细分析，其结果也可能不再是直线。

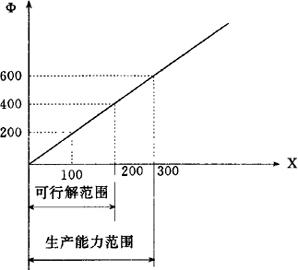
图2．1．6－3 目标函数与约束条件